はじめに
上の動画のように、プロシージャルに正多角形を描くことができるシェーダーの解説をしていきます。
UE5のマテリアルでの実装を例に解説しますが、仕組み部分は基本的にHLSLで書いているので、UnityでもGLSLとかでも簡単に再現できると思います。
プロシージャルに多角形を描く方法は色々あるかと思いますが、今回の手法は正多角形に限定される面はありつつ、かなり簡潔なロジックなので、個人的には気に入っています。
また、とりあえず現物が欲しいという人向けに、このシェーダーを実装したMaterialとストライプ等の簡易的な表現を入れたMaterial Instanceを以下のページで提供しているので、再現するのが面倒な人はチェックしてみてください。
https://heyyohanashima.gumroad.com/l/nmusq
解説
全体像
正多角形を描く部分の全体像としては、こんな感じです。
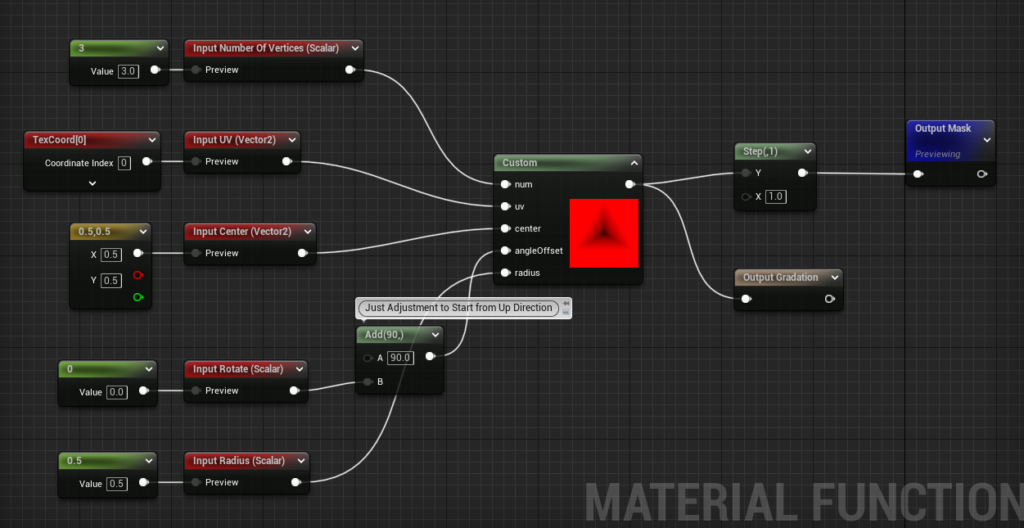
といっても処理のほとんどは、Customノード内でHLSLを使って実装しているので、コードを見せながら解説していきますが、その前にコンセプト部分の説明をします。
グラデーションを作る
今回の手法は、正多角形のマスクを作るにあたって、中心(重心)から各辺へのグラデーションを計算します。
中心から各辺に0→1になるグラデーションを作り、1を超えた部分を消す(透明にする)ことで各正多角形のマスクを作ります。

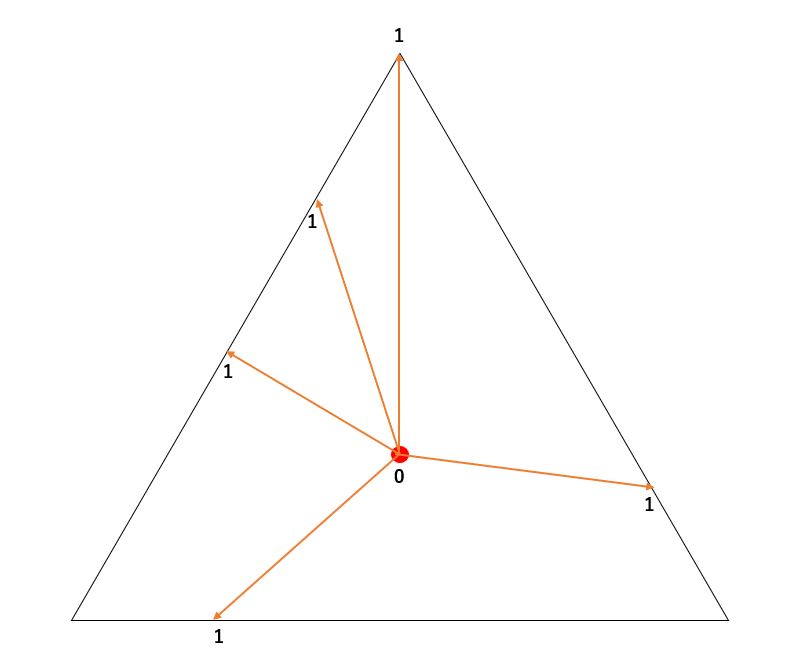
グラデーションの良い所は、ただマスクを作るだけでなく、色付けやフェードなどに使用できるので、活用の幅も広がります。
作成方針
中心から各辺へのグラデーションをどう作るかの方針を解説していきます。
キーとなるのは「内積」です。
CGのコンテキストで内積が話題になるとき、よく二つのベクトルの成す角度を求める利用方法が多いですが、実はまだ他にも重要な使い道があるので、解説します。
内積のおさらい
CG関連で自分が良く使う内積の性質は、2つあります。
① 二つのベクトルの成す角度
② 正射影ベクトルの長さ
どちらの性質も、内積の数式上の定義から導かれることですが、数式の説明はここではしないので、図を用いた簡単な説明にとどめます。
①の方は、シェーダー関連でいえば、フレネル計算だったり、簡易的な拡散・鏡面反射の計算で使われていて、よく話題に上がる内容かと思いますので、解説は割愛します。
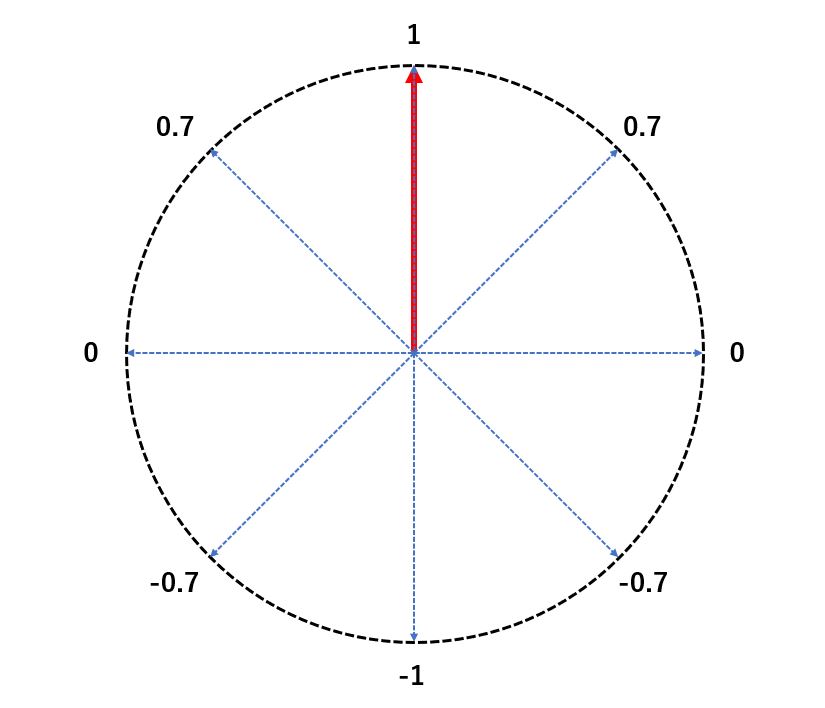
②の方が、今回利用する性質になります。
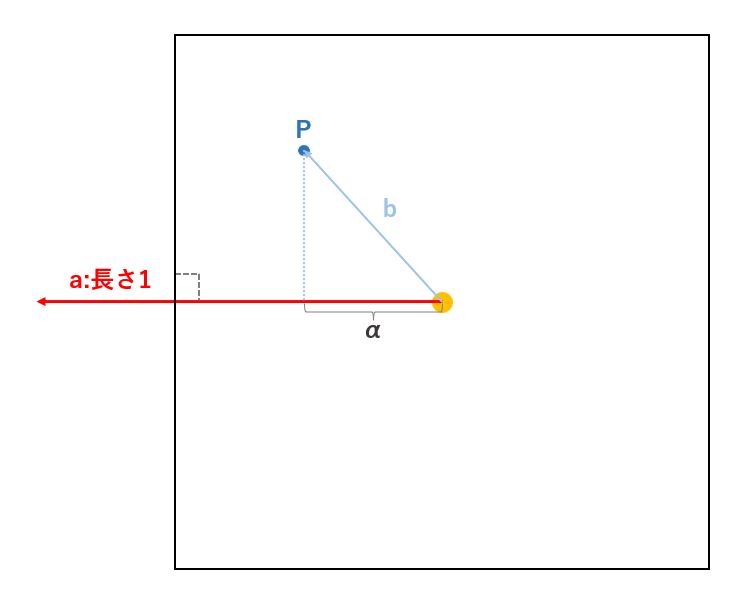
正射影ベクトルというちょっと難しい言葉が出てきましたが、図で見ればわかりやすいと思います。
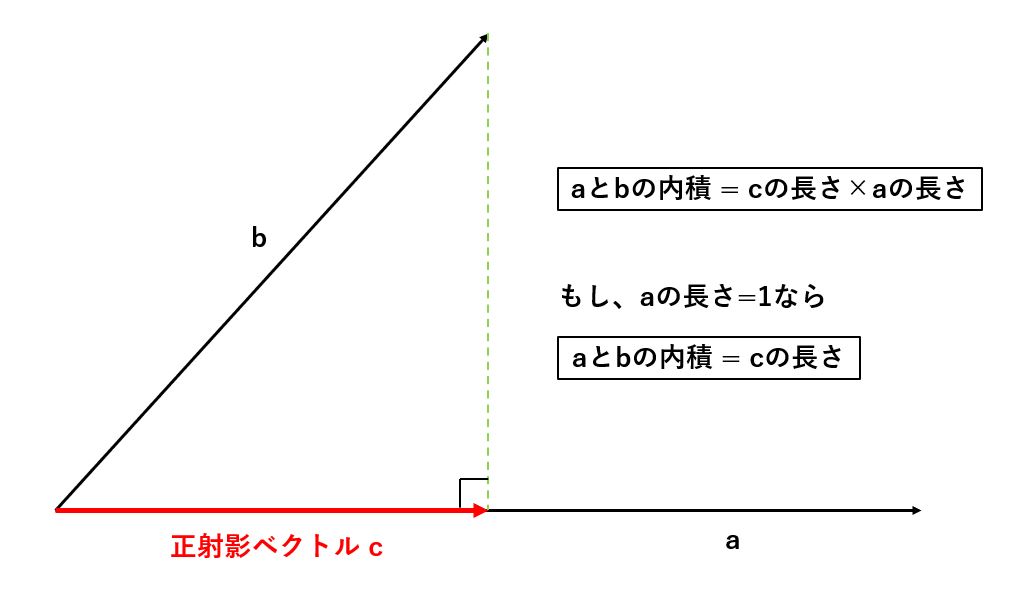
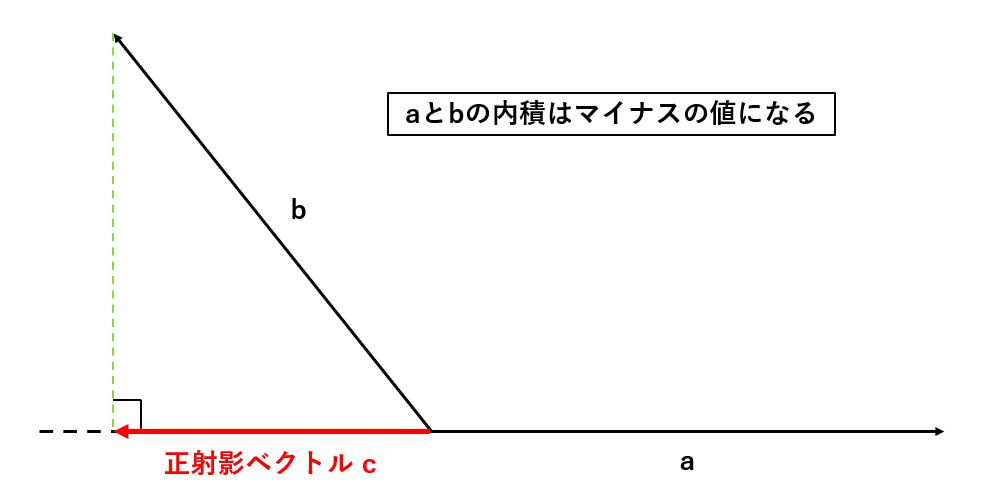
上の図のように、二つのベクトル(a,b)の始点を合わせて、片方のベクトル(b)の終点から、もう片方のベクトル(a)に対して垂直な線を引いたとき、始点からその交点へのベクトルを正射影ベクトル(c)と呼びます。
そして、aとbの内積は、この正射影ベクトルcの長さとベクトルaの長さの積になります。
この時、ベクトルaの長さを1にすることで、何に1を掛けても値は変わらないので、そのまま交点と始点の間の長さ(=正射影ベクトルの長さ)を求めることができます。
この性質を利用し、正多角形の中心から各辺へのグラデーションを計算することができます。
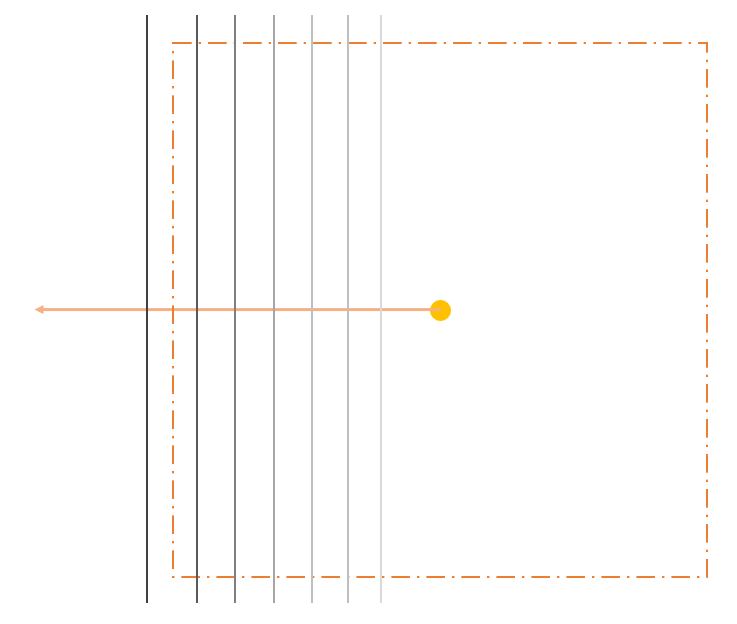
また、以下のようなベクトルの位置関係の場合、値はマイナスになります。
ちなみに、ベクトルaとかけ合わせれば正射影ベクトル自体も求められるので、こちらは、「特定の方向のベクトル成分をキャンセルしたい場合」などに使えたりもするので、覚えておくと良いと思います。
具体的な方針の解説
内積の解説も終わったので、具体的な方針の解説をします。
まず、正三角形を例にとって解説します。
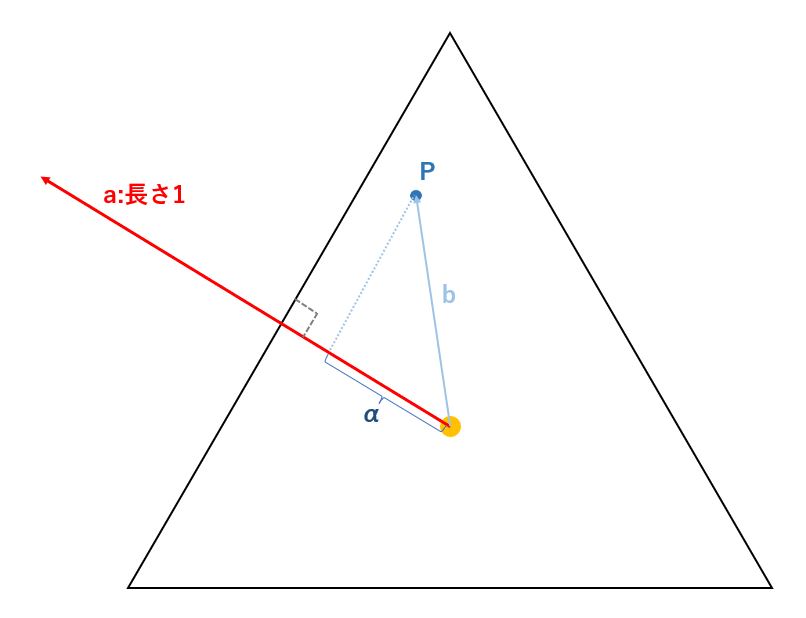
正三角形の中心から、辺に垂直な長さ1のベクトル(a)を求めます。
次に、正三角形の中心から任意の点(P)へのベクトル(b)を求めます。
このaとbのベクトルの内積を計算することで、ベクトルbの正射影ベクトルの長さ(α)を求めることができます。
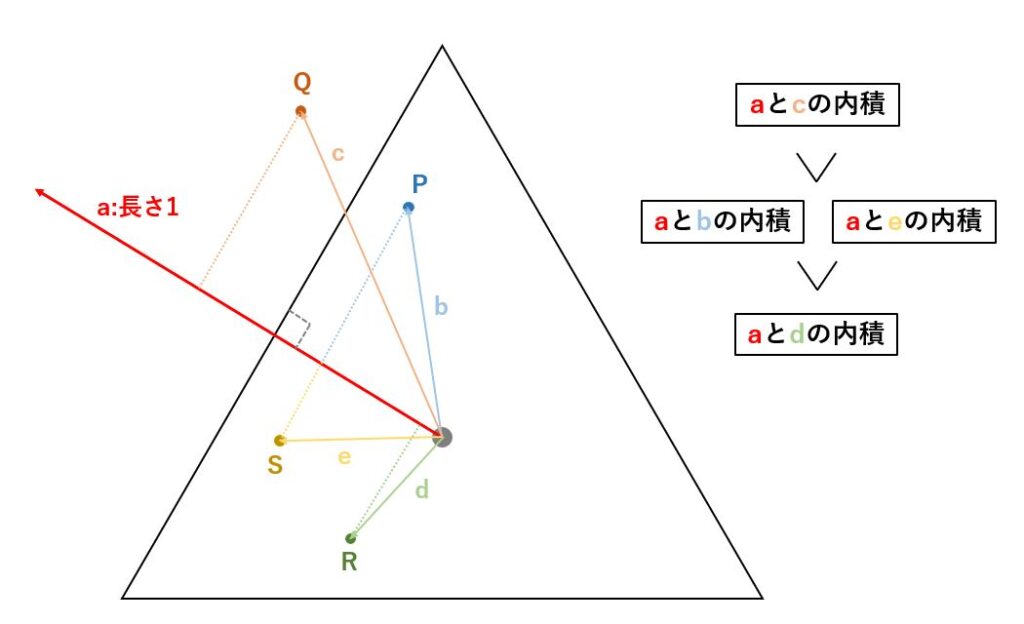
同様に、任意の点Q,R,Sに関しても同じ手順で計算することで、各点が中心から辺方向に遠ざかるほど大きな値になり、中心側に近づくほど小さな値になることがわかります。
また、PとSのように、辺に対して平行な線上にある点は、同じ正射影ベクトルの長さになることもわかります。
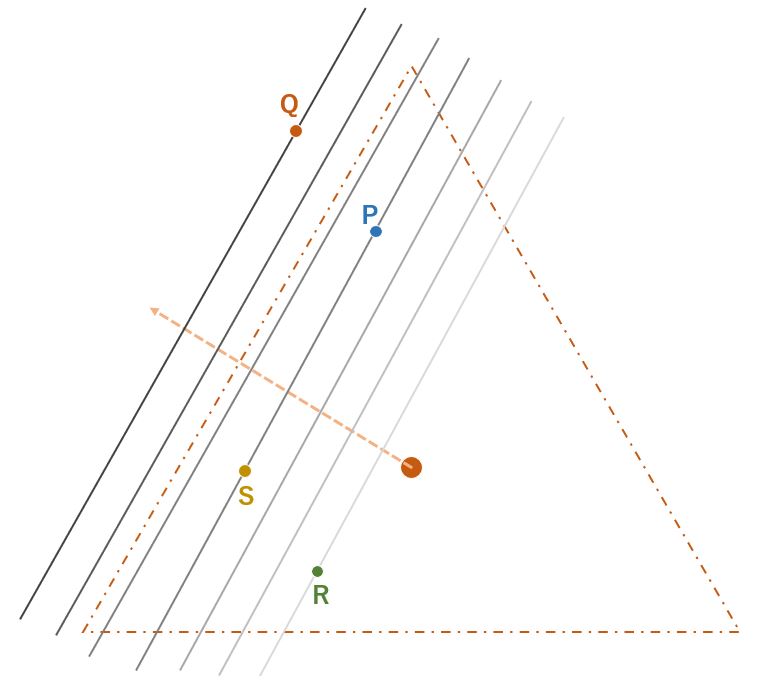
このように、内積を計算することで、辺に平行なグラデーションを得ることができます。
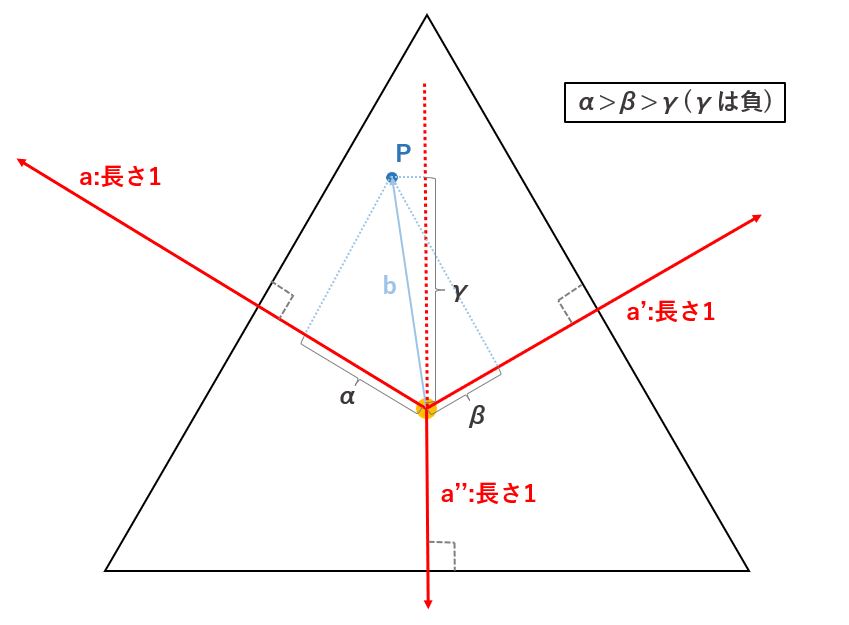
また、正三角形であれば、中心から各辺への垂直な線を3つ(a,a’,a”)引けますが、上の図のように、自身の点から一番近い辺に対して引かれたベクトルとの内積が、必ず一番大きい値になるので、実装上は、3つのベクトルとの内積を求めたうえで、一番大きい値を、その点のグラデーションとして使えば良いことになります。
そうすることで、以下のよう全辺に関して、各辺に平行なグラデーションを得ることができます。
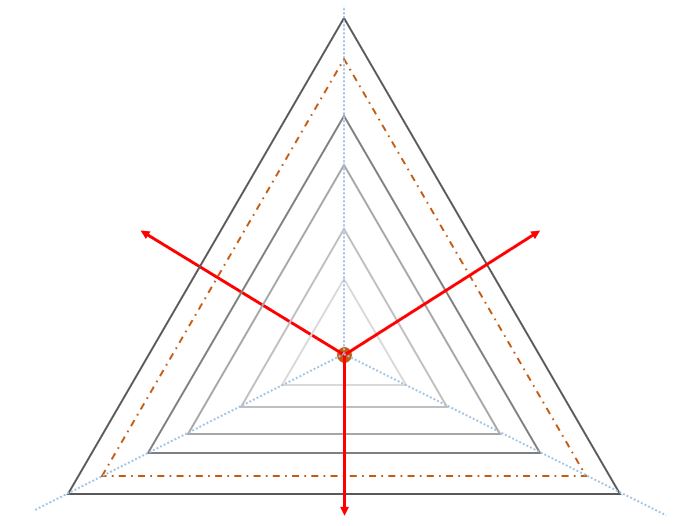
四角形の場合も同様の考えで、グラデーションを得ることができます。
そして、正多角形全て同様のロジックでグラデーションを得ることができます。
最後にグラデーションを作る手順をまとめます。
- 中心から各辺に垂直な長さ1のベクトルを求める
- 中心から任意の点へのベクトルと1のベクトルとの内積をとる
- 2の中で一番大きい値を、その点のグラデーション値とする
- 中心から辺への距離で、3の値を割り正規化(0~1)する
実装コードの解説
作成の方針を元に、実際のHLSLのコードを解説していきます。
まずは、コードの全文を載せます。
const float DEG_TO_RAD = 0.0174533;
int _num = max(num, 3); // Make sure more than 3 vertices
float _deltaAngle = 360.0 / (float)_num;
float2 _dir = uv - center;
float _gradAlongMedian = 0;
// Repeat calculation _num times and get max value of dot product
for(int i = 0; i < _num; i++) {
float _degree = angleOffset + _deltaAngle * i;
float _x = cos(_degree * DEG_TO_RAD);
float _y = sin(_degree * DEG_TO_RAD);
float2 _medianDir = normalize(float2(_x,_y));
_gradAlongMedian = max(dot(_medianDir, _dir), _gradAlongMedian);
}
float _centerToSideLength = radius * cos(_deltaAngle * 0.5 * DEG_TO_RAD);
float _normalizedMedianGradation = _gradAlongMedian / _centerToSideLength;
return _normalizedMedianGradation;インプットは、以下の5つです。
- num:頂点の数
- uv:正多角形を描く座標系
- center:中心座標
- angleOffset:正多角形の向きのオフセット
- radius:正多角形の大きさ(中心から頂点までの長さ)
アウトプットは、中心から各辺へのグラデーションを返します。
float _gradAlongMedian = 0;
// Repeat calculation _num times and get max value of dot product
for(int i = 0; i < _num; i++) {
float _degree = angleOffset + _deltaAngle * i;
float _x = cos(_degree * DEG_TO_RAD);
float _y = sin(_degree * DEG_TO_RAD);
float2 _medianDir = normalize(float2(_x,_y));
_gradAlongMedian = max(dot(_medianDir, _dir), _gradAlongMedian);
}ここで、頂点数(辺の数)だけ内積の計算をし、最大値を_gradAlongMedianに格納しています。
中心から各辺への垂線のベクトルは、まず360を頂点数で割って、各ベクトルの角度の差を計算した上で、三角関数で求めます。
float _centerToSideLength = radius * cos(_deltaAngle * 0.5 * DEG_TO_RAD);
float _normalizedMedianGradation = _gradAlongMedian / _centerToSideLength;中心から辺までの長さは、中心から頂点の長さに、cos(360/(頂点数×2))を乗算して求め、_gradAlongMedianを割って、正規化します。
これで、中心から各辺に向かって、0→1になるグラデーションを得ることができ、_normalizedMedianGradation>1となる点は、求めている正多角形の外側に位置することになります。
グラデーションを使う
マスクする
上述の通り、外側にある点は1より大きくなるようなグラデーションを作ったので、stepを使って、1より大きい所を消せば、正多角形のマスクを作ることができます。
色を付ける・ストライプを作る
グラデーション情報があるので、色付けなどはいかようにもできます。詳細は割愛しますが、fmodなどを使えばストライプも簡単に作成できます。
おわりに
仕事で、UE内でモーショングラフィック的なことをする機会があったので、primitiveな形の大きさや回転など簡単に弄りたく、このシェーダーを作るに至りました。
やはり、きれいなロジックで汎用的なものが作れると気持ちがいいものですね。また、今まで知らなかった数学の知識の使い道に気が付くのも嬉しいものです。これからも、まだまだ隠された数学の使い道を探求していきたいと思います!



